What is a Pugh Matrix?
Smartpedia: The Pugh matrix, named after Stuart Pugh, is a decision aid for evaluating competing concepts in comparison to a basic concept.
Pugh Matrix – identification of the best possible solution
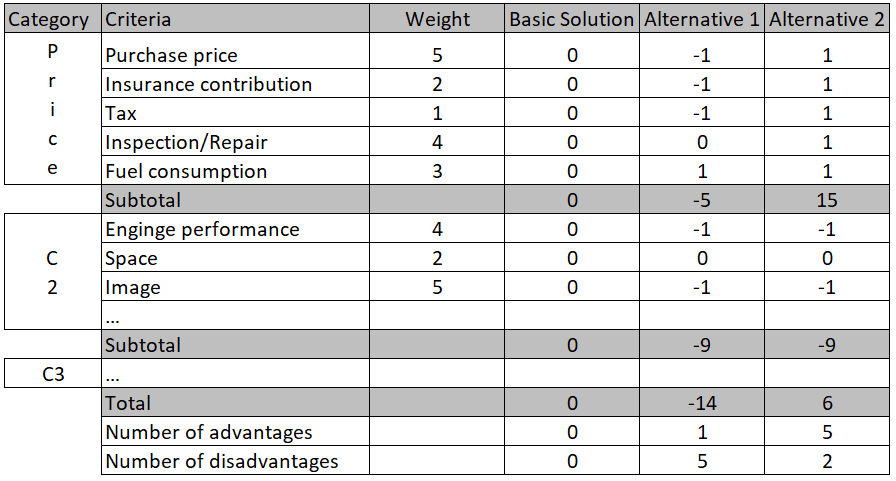
The Pugh Matrix, named after its inventor Stuart Pugh, is a decision-making aid for evaluating competing concepts in comparison to a basic concept. It is based on a set of defined, weighted criteria, the evaluation of alternatives in comparison to a basic solution, the multiplication of the evaluations with the respective weightings and the subsequent addition of the weighted evaluations. The Pugh Matrix, also known as the Pugh Method, Pugh Analysis, Pugh Concept, Pugh Controlled Convergence or decision-matrix method, consists of a table with the following columns:
- Column 1: Category of the evaluation criteria used to structure the decision matrix and form subtotals.
- Column 2: List of evaluation criteria.
- Column 3: Weighting of the criteria, e.g. from 1 to 5 or from 1 to 10. The more important the criterion is, the higher the weighting. The more gradations there are, the more precise the weighting of the criteria can be. Ideally, the evaluation criteria should be weighted before the solution concepts are evaluated. (As an extension of the Pugh Matrix, the categories could also be weighted additionally.)
- Column 4: The basic concept is a baseline with a collective rating of 0 per evaluation criterion.
- Column 5 and following: Presentation of various solution concepts including comparison with the baseline. There are different variants here: If 3 values are used, 0 means as good as the basic concept, -1 means worse and +1 means better than the basic concept. When using 5 values +2 means much better, +1 means better, 0 means equally good, -1 means worse and -2 means much worse than the basic concept. With 7 values, the scale ranges from +3 to -3.
The objectivity of the Pugh Matrix
As with any weighted decision matrix, the Pugh matrix cannot guarantee that all criteria, weightings and assessments are objectively selected and made. Nevertheless, the Pugh Matrix tries to objectify decision making and is therefore universally applicable in many areas. The special thing about the Pugh Matrix is the pairwise comparison, in which an alternative is always compared with the basic concept. This can lead to a very precise differentiation.
Notes:
If you are interested in other prioritisation methods besides the Pugh matrix, we recommend you download the prioritisation whitepaper free of charge.
If you like the article or would like to discuss it, please feel free to share it in your network. And if you have any comments, please do not hesitate to send us a message.
Here you will find additional information from our Smartpedia section: